Задача 5.
Незнайка измерил длины сторон и диагоналей своего четырёхугольного земельного участка, записал в блокнот результаты шести измерений и тут же забыл, какие числа относились к диагоналям, а какие — к сторонам. Потом он заметил, что среди написанных чисел есть четыре одинаковых, а два оставшихся числа тоже равны между собой. Незнайка обрадовался и сделал вывод, что его участок — квадрат. Обязательно ли это так? Если ответ «да», то утверждение нужно доказать, если ответ «нет» — привести опровергающий пример и его обосновать.
Ответ на Задачу 5.
Ответ: Нет, необязательно.
Решение:
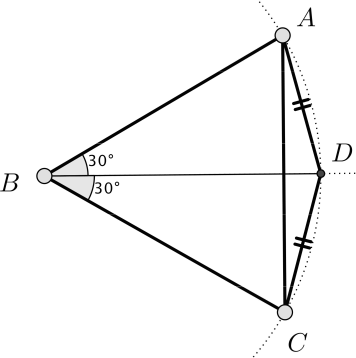
Построим равносторонний треугольник $ABC$ и на биссектрисе его угла $B$ отложим отрезок $BD$, равный $AB$. В четырёхугольнике $ABCD$ имеем $AB$ = $BC$ = $CA$ = $BD$ (по построению) и $AD$ = $DC$ (например, из равенства треугольников $BAD$ и $BCD$ по двум сторонам и углу между ними). Очевидно, что построенный четырёхугольник не является квадратом (например, так как угол $ABC$ равен 60°). Участок Незнайки мог иметь форму этого четырёхугольника.
Замечание. Возможен и участок невыпуклой формы, обладающий теми же свойствами.

