Задача 5.
Квадратный оконный проём образован трёмя прямоугольными рамами (см. рисунок ниже). Внутри каждой из них написали число, равное периметру рамы. Напишите, чему равна сторона квадрата всего оконного проёма и объясните, как вы её получили.
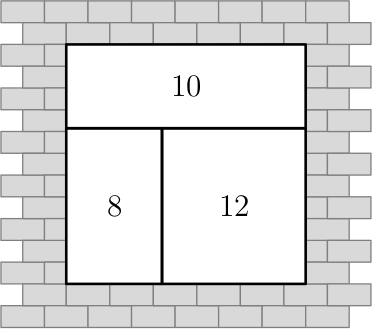
Ответ на Задачу 5.
Ответ: 4.
Решение:
Пусть сторона квадрата равна $a$, а высота левого нижнего проёма равна $b$, ширина левого нижнего проёма равна $c$. Тогда высота верхнего прямоугольника равна $a$ − $b$, ширина равна $a$; высота правого прямоугольника равна $b$, ширина равна $a$ − $c$. Выпишем соотношения периметров трёх прямоугольников:
2$a$ + 2$a$ − 2$b$ = 10;
2$b$ + 2$c$ = 8;
2$b$ + 2$a$ − 2$c$ = 12.
Сложим два последних равенства, получим 2$a$ + 4$b$ = 20. Прибавим к результату удвоенное первое равенство, останется 10$a$ = 40, откуда $a$ = 4.

