Задача 2.
Радиус описанной окружности равнобедренного треугольника $ABC$ ($AB$ = $BC$) равен основанию $AC$. На основании $AC$ построен квадрат $AKLC$ так, что отрезок $KL$ пересекает боковые стороны треугольника. Докажите, что треугольник $BKL$ равносторонний.
Ответ на Задачу 2.
Решение: Отметим точку $O$ — центр описанной окружности треугольника $ABC$. Из условия получим, что $OA$ = $OC$ = $AC$, то есть треугольник $AOC$ равносторонний. Поскольку $AKLC$ — квадрат, имеем $AK$ = $KL$ = $LC$ = $AC$. Заметим, что $BO$ ∥ $LC$, поскольку обе прямые перпендикулярны $AC$, и также $BO$ = $LC$ (см. рисунок).
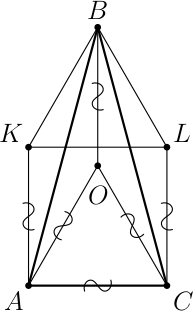
Это означает, что $OBLC$ — параллелограмм. Тогда получаем, что $OC$ = $LB$. Аналогично получаем, что $KB$ = $AO$. Итого получаем, что $KB$ = $BL$ = $KL$, что и требовалось доказать.

