Задача 8.
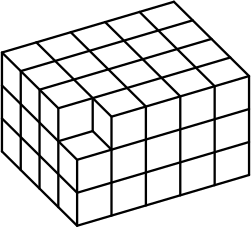
Конфеты имеют форму кубиков 1 × 1 × 1. Учитель сложил из них параллелепипед 3 × 4 × 5 и предложил детям угощаться. В первую минуту Петя взял одну из угловых конфет (см. рисунок). Каждую следующую минуту дети забирали все конфеты, у которых была соседняя грань с уже отсутствующими конфетами (например, во вторую минуту забрали 3 конфеты). За сколько минут дети разобрали все конфеты?
Ответ на Задачу 8.
Ответ: За 10 минут.
Решение:
Ответом будет число шагов, которым можно добраться из отмеченного угла в наиболее удалённый от него угол, переходить при этом можно только через грань кубика. Это число шагов не зависит от траектории, по которой мы будем добираться из одного угла в другой, и будет равно 10.
Пример траектории: отмеченный кубик + 4 шага от отмеченного кубика по длинной стороне + 3 шага по короткой стороне + 2 шага вниз = 1 + 4 + 3 + 2 = всего 10 кубиков пройдено. Первый кубик забрали в первую минуту, значит последний 10-й кубик заберут в 10-ю минуту.

