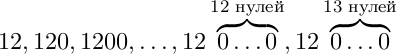Задача 7.
У дракона есть 40 кучек золотых монет, в любых двух из них количество монет отличается. После того как дракон разграбил соседний город и принёс ещё золото, количество монет в каждой кучке увеличилось либо в 2, либо в 3, либо в 4 раза. Какое наименьшее количество различных кучек монет могло получится?
Ответ на Задачу 7.
Ответ: 14 кучек.
Решение:
Оценка. Предположим, что не более 13 кучек увеличилось в одинаковое количество раз. Тогда не более 13 кучек увеличилось в 2 раза, не более 13 — в три раз, не более 13 — в 4 раза. Таким образом у дракона всего не более 39 кучек. Противоречие.
Таким образом, найдутся 14 кучек, количество монет в которых увеличилось в одинаковое количество раз. Раз в этих кучках первоначально было различное количество монет, то и в итоге будет различное количество монет.
Пример. Пусть у дракона первоначально были кучки со следующим количеством монет:

В каждой кучке со знаменателе 2 он увеличил количество монет в 2 раза, в каждой кучке со знаменателем 3 — в 3 раза, со знаменателем 4 — в 4 раза. После этого у него будет 14 различных значений: