Всероссийская олимпиада школьников по математике, 9 класс, 2019 год
дата проведения: 14 октября 2019 - 20 октября 2019
Задача 5.
На стороне $AD$ квадрата $ABCD$ отметили точку $K$, а на продолжении луча $AB$ за точку $B$ – точку $L$. Известно, что $\angle LKC$ = 45°, $AK$ = 1, $KD$ = 2. Найдите $LB$.
Ответ на Задачу 5.
Ответ: $LB$ = 2.
Решение:
Решение: Заметим, что $∠LAC$ = 45° = $∠LKC$, откуда следует, что четырёхугольник $LAKC$ вписанный. Тогда $∠KCL$ = 90° (см. рисунок).
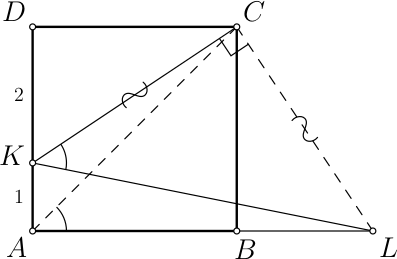
Значит, треугольник $LCK$ равнобедренный прямоугольный, т.е. $LC$ = $KC$. Прямоугольные треугольники $BLC$ и $DKC$ равны по гипотенузе и катету, поэтому $BL$ = $KD$ = 2.

