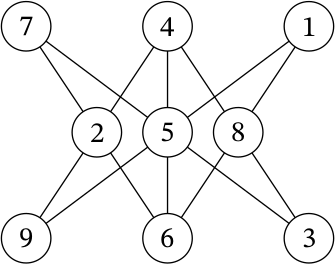
Задача 4.
Расставьте цифры от 1 до 6 (каждую нужно использовать ровно один раз) так, чтобы сумма трёх чисел, расположенных на каждой из 7 прямых, была равна 15. В ответе укажите, какие цифры должны стоять на местах 𝐴 – 𝐹.
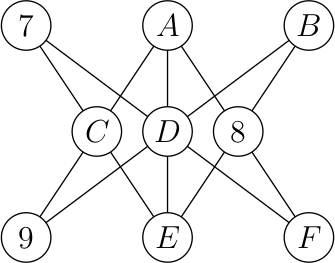
Ответ на Задачу 4.
Ответ: 𝐴 = 4, 𝐵 = 1, 𝐶 = 2, 𝐷 = 5, 𝐸 = 6, 𝐹 = 3.
Решение:
По условию 𝐴, 𝐷, 𝐸 — различные цифры, не превосходящие 6, сумма которых равна 15. Если эти цифры брать максимально возможными, то их сумма 4 + 5 + 6 = 15. Значит, 𝐴, 𝐷, 𝐸 — это 4, 5, 6 в некотором порядке (если хотя бы одна из цифр не больше 3, то сумма всех трёх цифр не больше 3 + 5 + 6 < 15).
При этом 𝐴 ≠ 6 (иначе 𝐴 + 𝐶 + 9 > 15) и 𝐷 ≠ 6 (иначе 𝐵 + 𝐷 + 9 > 15). Следовательно, 𝐸 = 6.
Поскольку 7 + 𝐶 + 𝐸 = 15 и 𝐸 = 6, получаем 𝐶 = 2.
Поскольку 9 + 𝐶 + 𝐴 = 15 и 𝐶 = 2, получаем 𝐴 = 4.
Поскольку 𝐴 + 8 + 𝐹 = 15 и 𝐴 = 4, получаем 𝐹 = 3.
Поскольку 7 + 𝐷 + 𝐹 = 15 и 𝐹 = 3, получаем 𝐷 = 5.
Поскольку 9 + 𝐷 + 𝐵 = 15 и 𝐷 = 5, получаем 𝐵 = 1.