Задача 7.
Мышонок Джерри решил подарить коту Тому на День Рождения пирог в виде квадрата 8 × 8. В три куска, отмеченные буквой «Р», он положил рыбу, в два куска, отмеченные буквой «К», положил колбасу, а ещё в один кусок добавил и то, и другое, но такой кусок не отметил (все остальные куски — без начинки). Также Джерри сообщил Тому, что в любом квадрате 6 × 6 есть хотя бы 2 куска с рыбой, а в любом квадрате 3 × 3 — не более одного куска с колбасой.
Какое наименьшее количество кусков пирога надо съесть Тому, чтобы среди них гарантированно оказался кусок с рыбой и колбасой?
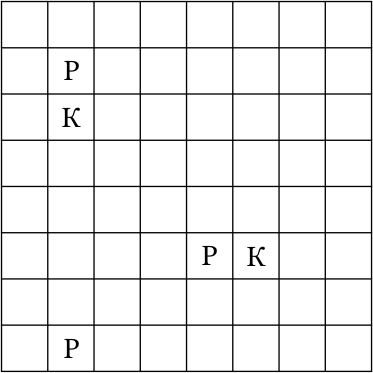
Ответ на Задачу 7.
Ответ: 5 кусков.
Решение:
Кусок с рыбой и колбасой назовём заветным. По условию в любом квадрате 6 × 6 есть хотя бы 2 куска с рыбой. В любом таком квадрате хотя бы один известный кусок с рыбой уже содержится; рассмотрим те квадраты, которые содержат только 1 известный кусок рыбы (все они прилегают к правой границе пирога). Можно увидеть, что у них есть общий прямоугольник 4 × 6 (серый на рисунке). Значит, именно в нём и содержится заветный кусок.
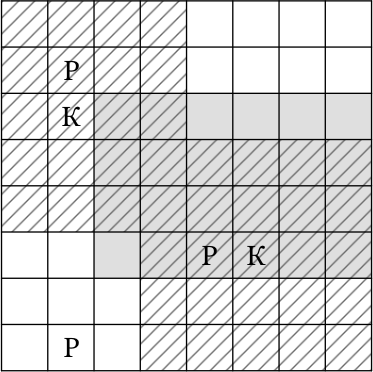
Далее, по условию в любом квадрате 3 × 3 не более 1 куска с колбасой. Значит, в любом таком квадрате, который уже содержит известный кусок колбасы, заветного куска не будет. Такие квадраты закрывают области 5 × 5 с центрами в каждом куске колбасы (заштрихованы на рисунке).
Остаётся ровно 5 клеток (серых, но не заштрихованных). Несложно проверить, что каждый из этих 5 случаев удовлетворяет условию задачи. Если Том съест не более 4 кусков пирога, то одна из перечисленных выше пяти клеток точно окажется не тронута, а в ней может находиться заветный кусок. А если Том съест 5 кусков в этих клетках, то среди них точно будет заветный.

