Задача 8.
Есть 7 абсолютно одинаковых кубиков, у которых отмечены на одной грани 3 точки, на двух гранях по 2 точки, на остальных по 1. Из этих кубиков склеили фигуру в виде буквы «П», изображённую на рисунке, причём количество точек на любых двух соприкасающихся гранях одинаково.
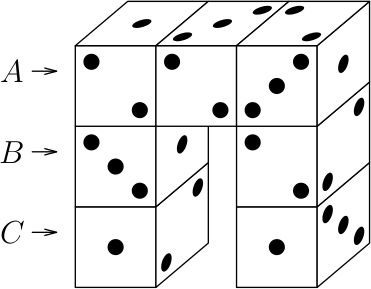
Что находится на трёх левых гранях 𝐴, 𝐵 и 𝐶?
Ответ на Задачу 8.
Ответ: 𝐴 — 2, 𝐵 — 2, 𝐶 — 3.
Решение:
Для полного решения этой задачи необходимо не только понимание того, сколько точек расположено на гранях кубика и какие именно из них соседние. Также важно разобраться в том, по каким именно диагоналям направлены точки на гранях кубика.
Рассмотрим правый средний кубик (над и под которым есть ещё кубики). На его верхней грани, как и на его нижней грани, не могут стоять 3 точки (иначе у верхнего или у нижнего кубика было бы хотя бы две грани по 3 точки). Значит, грань с 3 точками — одна из двух оставшихся (которые не видны и ни с кем не соприкасаются). Тогда в нашем кубике напротив грани с 3 точками находится грань с 2 точками, одна из четырёх оставшихся граней имеет 2 точки, а остальные три — по 1 точке.
Рассмотрим средний верхний кубик. На верхней его грани 3 точки, на ближней — 2 точки. Ясно, что тогда на нижней грани этого кубика 2 точки, а на левой — 1 точка (см. рисунок).
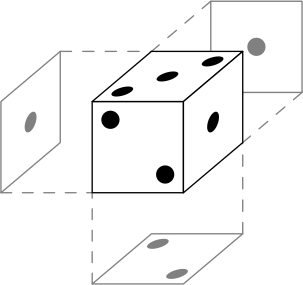
На рисунке чёрным изображены три «настоящие» грани кубика; серым — вынесенные изображения трёх остальных граней.
Рассмотрим средний верхний кубик и левый средний. Они абсолютно одинаковые, поэтому их можно совместить в пространстве («наложить» друг на друга). При этом грани с трёмя точками должны совместиться; с учётом направлений этих точек понятно, что это можно сделать только двумя способами; один из этих способов невозможен, так как иначе видимая грань с 2 точками совместится с видимой гранью с 1 точкой. Значит, положение левого среднего кубика определено однозначно, и на его левой грани 𝐵, а также на задней грани по 2 точки. Тогда на его верхней и нижней грани по 1 точке.
У верхнего кубика верхняя, передняя и нижняя грань определены. Правая тоже — на ней 1 точка, т.к. на левой грани верхнего среднего кубика 1 точка. Тогда на грани 𝐴 обязательно 2 точки, а на задней грани — 3 точки.
У нижнего кубика на передней и верхней грани по 1 точке, а на правой 2. Поскольку напротив грани с 3 точками не может находиться грань с 1 точкой, получаем, что на грани 𝐶 3 точки.
Итак, на грани 𝐴 находятся 2 точки, на грани 𝐵 — 2 точки, на грани 𝐶 — 3 точки. Несложно убедиться, что все 7 кубиков можно расположить так, как на рисунке, чтобы все условия задачи выполнялись.

