Задача 6.
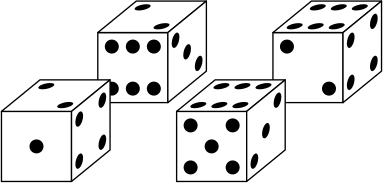
Есть 4 абсолютно одинаковых кубика, у каждого из которых на одной грани отмечены 6 точек, на другой — 5, …, на оставшейся — 1. Известно, что на любых двух противоположных гранях кубика суммарно 7 точек.
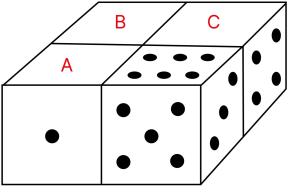
Из этих 4 кубиков склеили фигуру, изображённую на рисунке. Известно, что на каждой паре склеенных граней отмечено одинаковое количество точек. Сколько точек на гранях 𝐴, 𝐵, 𝐶?
Ответ на Задачу 6.
Ответ: 𝐴 = 2, 𝐵 = 2, 𝐶 = 6.
Решение:
Сначала воспользуемся условием о том, что сумма количеств точек на паре противоположных граней кубика равна 7, чтобы понять, как выглядит кубик, три грани которого нам известны. Его скрытые грани изображены на рисунке ниже (с точностью до расположения точек на грани с 2 точками, которое из условия однозначно определить нельзя — но в решении данной задачи оно роли и не играет).
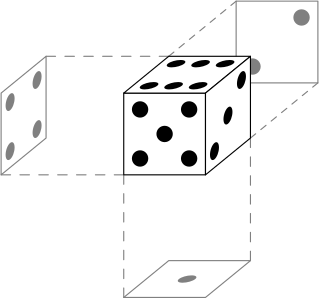
Мы знаем, что остальные кубики точно такие же. У каждого из кубиков с гранями 𝐴 и 𝐶 одну грань мы видим, а ещё одну грань знаем, так как она склеена с известной гранью первого кубика. По расположению двух соседних граней можно однозначно установить ориентацию кубика в пространстве. После этого станут известны две грани кубика 𝐵, которыми он склеен с кубиками 𝐴 и 𝐶, и мы аналогично установим его ориентацию. Кубики в раздвинутом виде изображены на рисунке ниже (опять-таки с точностью до расположения точек на гранях с двумя точками).