На большой ферме живут 630 кроликов. В один из дней фермер покормил их из расчёта 3 килограмма моркови на 70 кроликов, а надо было — 7 килограммов моркови на 90 кроликов. Сколько ещё моркови понадобится, чтобы правильно накормить кроликов? Ответ выразите в килограммах.

Лёня разрезал по линиям сетки прямоугольник 7 × 4 на семь прямоугольников площадью 6, 5, 5, 5, 4, 2, 1. Площадь каждого из первых шести прямоугольников Лёня написал в одной из его клеток, как показано на рисунке.

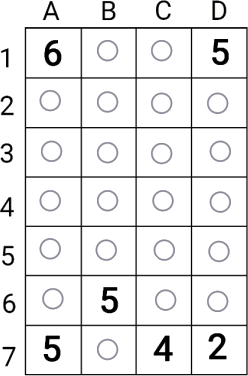
Какой клетке соответствует прямоугольник площади 1?

Учитель выписал на доску несколько подряд идущих натуральных чисел, начиная с единицы. Петя заметил, что ровно 17 из них делятся на 3, а Вася заметил, что ровно 3 из них делятся на 13. Сколько чисел выписал на доску учитель?

У Ильи есть 16 фигурок солдатиков: лучников и мечников. Если он отдаст брату любые 3 фигурки, то мечников у него останется в любом случае больше, чем лучников. Если же он отдаст брату половину мечников, то лучников у него останется больше, чем мечников. Сколько фигурок лучников у Ильи?

Найдите наибольшее восьмизначное число, удовлетворяющее двум условиям:

• У него любые три подряд идущие цифры различны;
• У него произведение любых трёх подряд идущих цифр делится на 20.

На рисунке изображён прямоугольник, разрезанный на семь квадратов.

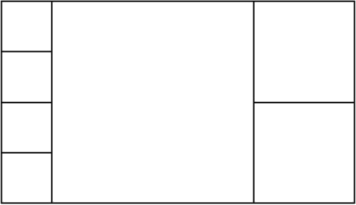
Найдите периметр этого прямоугольника, если его площадь равна 2268.

У Вани есть 234 монеты и доска 7 × 7. Он разложил все монеты в клетки доски так, что в любых четырёх клетках, образующих прямоугольник 1 × 4 или 4 × 1, суммарно оказалось ровно 19 монет (в каких-то клетках могло оказаться несколько монет, а какие-то клетки могли оказаться пустыми).

Сколько всего монет может находиться в четвёртом столбце? Укажите все возможные варианты.

На острове живут рыцари, которые всегда говорят правду, и лжецы, которые всегда лгут. Однажды собрались на заседание 50 жителей острова, среди которых было 𝑘 лжецов (𝑘 ≥ 4). Все лжецы по очереди сделали заявления:

• Первый лжец: «Среди нас рыцарей меньше, чем лжецов»,
• Второй лжец: «Среди нас рыцарей столько же, сколько лжецов»,
• Третий лжец: «Среди нас рыцарей на 1 больше, чем лжецов»,
• Четвёртый лжец: «Среди нас рыцарей на 2 больше, чем лжецов»,
• ...
• 𝑘-й лжец: «Среди нас рыцарей на (𝑘 − 2) больше, чем лжецов».

Найдите наибольшее возможное значение 𝑘.