Задача 1.
Отметьте в квадрате 6 × 6 несколько клеток так, чтобы в каждой строке количество отмеченных клеток соответствовало числу, записанному слева от неё, а в каждом столбце — числу, записанному сверху от него.
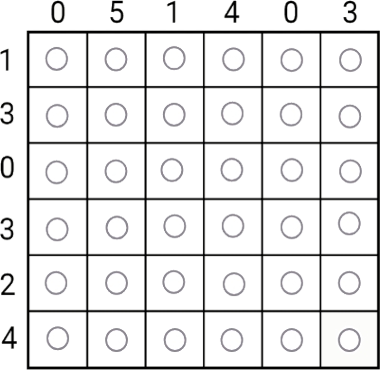
Задача 2.
Футбольный матч закончился со счётом 5:1. Каждый гол в этом матче был устроен так: один игрок давал голевой пас своему сокоманднику, а тот забивал гол команде соперников.
После каждого гола в протокол матча записывали имена двух игроков из одной команды: того, кто забил гол, и того, кто отдал голевой пас. По итогу матча в протоколе оказались записаны имена только четырёх игроков: Андрея, Бориса, Вадима и Дениса. Сколько забил голов и сколько отдал голевых передач Денис, если известно, что его сокомандник Андрей забил ровно 3 гола?
Задача 3.
В большой кроличьей семье есть дети: кролики и крольчихи. У каждого кролика братьев в 2 раза больше, чем сестёр. А у каждой крольчихи сестёр на 9 меньше, чем братьев. Сколько всего детей в этой семье?
Задача 4.
У мальчиков Ильи, Максима, Вовы и Лёши есть конфеты: 1, 2 или 3 у каждого. Они заявили следующее:
- Илья: «У Вовы не 1 конфета».
- Максим: «Ровно у двоих из нас по 3 конфеты».
- Вова: «Количества конфет у Максима и Лёши отличаются не более чем на 1».
- Лёша: «У меня конфет больше, чем у Вовы».
Известно, что соврал только один мальчик, и он — единственный, у кого 1 конфета. У кого сколько конфет?
Задача 5.
Квадрат на рисунке разбит на 11 меньших квадратов: белых и серых. Суммарная площадь серых квадратов равна 204. Чему равна суммарная площадь белых квадратов?

Задача 6.
По обе стороны дороги стоят столбы так, что расстояние между первым и последним столбами с каждой стороны равно 37 км. С левой стороны стоит 125 столбов, и расстояние между соседними столбами одинаковое. С правой стороны расстояние между соседними столбами тоже одинаковое, но оно на треть больше, чем с левой. Сколько всего столбов стоит справа?
Задача 7.
На рисунке изображена клетчатая доска. Будем считать, что фишка на этой доске видит другую фишку, если они расположены либо в одной вертикали, либо в одной горизонтали, причём между ними нет границ доски. Сколькими способами можно расставить 5 фишек на этой доске так, чтобы никакие две из них не видели друг друга?
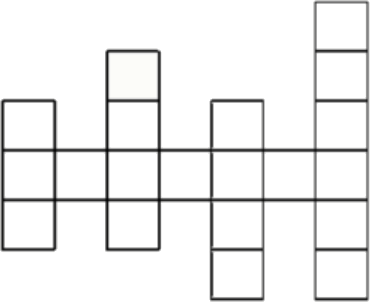
Задача 8.
Андрей, Боря, Вера, Галя, Денис и Елена решили сыграть в настольную игру. Они разбились на три команды, каждая из которых состоит из мальчика и девочки. Цель игры — получить как можно больше очков.
К концу игры все дети суммарно набрали 151 очко, причём в каждой команде девочка набрала на 5 очков больше, чем мальчик. При этом если к числу очков Андрея прибавить число очков Гали, то получится 52, а если прибавить число очков Веры, то получится 48. Известно, что каждый из детей набрал целое число очков. Сколько очков набрала Елена?

