Два арбуза, дыня и четыре нектарина стоят 1000 рублей, а арбуз, две дыни и два нектарина — на 50 рублей дешевле. Сколько стоит набор из арбуза, дыни и двух нектаринов? Ответ выразите в рублях.

Персонаж Ральф живёт в компьютерной игре, поэтому озёра в его мире имеют форму клетчатых фигур, показанных на рисунке.

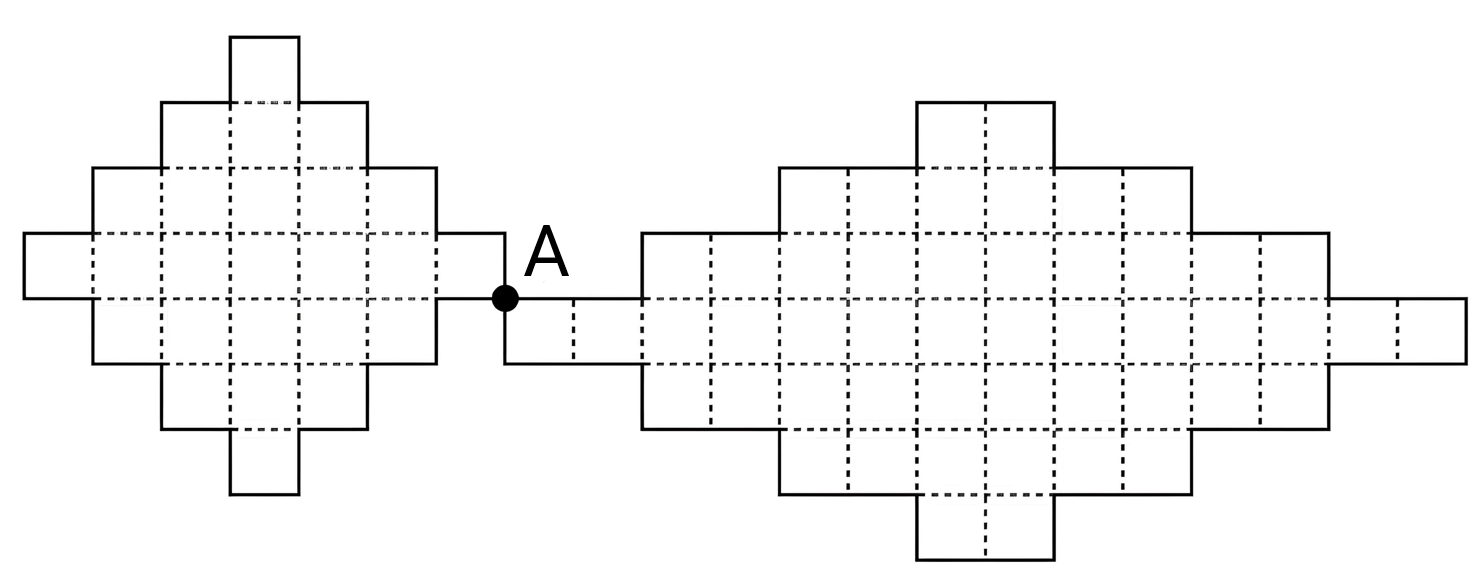
Каждое утро Ральф идёт на пробежку вдоль берега одного из двух озёр: начинает в точке A, бежит с постоянной скоростью и заканчивает, когда вновь оказывается в A. Известно, что озеро размером в одну клетку персонаж обежал бы за 2 минуты. На сколько минут одна пробежка Ральфа длится дольше другой?

По кругу расставлены шестьдесят горшков. В каждом из горшков сидит хотя бы одна лягушка, и в любых трёх стоящих подряд горшках суммарно сидит ровно четыре лягушки. Сколькими способами цапля Анастасия сможет выбрать два горшка так, чтобы в них суммарно оказалось ровно три лягушки?

Аделина, Эвелина и Паулина писали олимпиаду по математике, где за каждую задачу можно было получить некоторое целое неотрицательное количество баллов. После объявления итогов выяснилось, что Аделина и Эвелина показали одинаковый результат, а сумма их баллов больше 15. Сумма баллов всех трёх девочек оказалась меньше 60 и в 3$\dfrac{1}{3}$ раза больше, чем набрала Паулина. Сколько баллов на олимпиаде набрала Аделина?

В футбольном турнире принимали участие 35 команд, среди которых команды «Белка» и «Стрелка». Правила футбольного турнира следующие: каждая команда играет с каждой по одному разу, в каждом матче победившая команда получает 3 очка, а проигравшая — 0 очков, в случае ничьей обе команды получают по 1 очку. По результатам турнира команда «Белка» набрала 100 очков, а команда «Стрелка» со всеми командами сыграла вничью. Какая наибольшая сумма очков могла быть у команды, занявшей второе место по результатам турнира?

По кругу стоят N человек, пронумерованных по часовой стрелке от 1 до N. Первый, третий, пятый и так далее до конца нумерации сказали: «Мой сосед слева — рыцарь». Второй, четвёртый, шестой и так далее до конца нумерации сказали: «Мой сосед слева — лжец». Чему может быть равно число N? Соседом слева называется следующий по часовой стрелке человек. Укажите все возможные варианты.

На каждом шаге к данному числу можно прибавить единицу или удвоить его. За какое наименьшее число шагов из числа 1 можно получить число 51?

Сколько существует натуральных чисел, в 23 раза больших своего наименьшего собственного делителя? Делитель называется собственным, если он больше 1, но меньше самого числа.