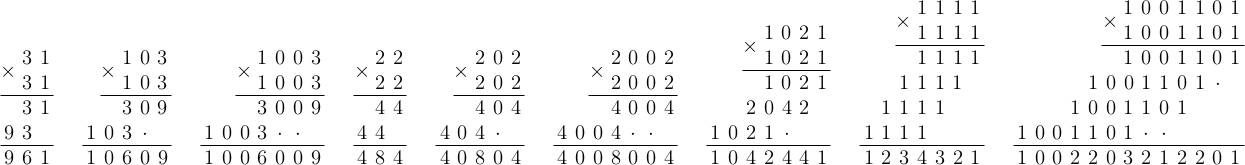Задача 1.
Сумма цифр некоторого 100-значного числа равна 4. Какой может быть сумма цифр квадрата, этого числа? (Найдите все ответы и докажите, что других ответов нет.)
Ответ на Задачу 1.
Ответ: 7 или 16.
Решение:
В числе не может быть цифр, больших 4. Если среди цифр есть 4, то число равно 40 . . . 0, и его квадрат имеет вид 160 . . . 0, а сумма цифр равна 7.
Если в числе нет цифры 4, то все цифры меньше или равны 3. Будем возводить число в квадрат, умножая его на себя в столбик. Для этого нужно каждую ненулевую цифру числа умножить на само число и получившиеся строки после необходимых сдвигов сложить. При умножении цифры на число не будет ни одного переноса через разряд, так как нет цифр, больших 3. То есть умножение числа на его цифру можно выполнять «порязрядно», а сумма цифр у получившегося произведения равна самой цифре, умноженной на 4. Если в результате сложения этих строк не будет ни одного переноса через разряд, то сумма цифр ответа будет равна квадрату суммы цифр исходного числа (то есть 16). Можно показать, что переносов не будет, но проще заметить, что при сложении каждый перенос через разряд уменьшает сумму цифр на 9. Поэтому могут получиться только суммы 16 и 16 − 9 = 7. Сумма цифр 16 получается, например, для числа 310.
Примеры умножения в столбик чисел, все цифры которых не превосходят 3: