Сумма цифр некоторого 100-значного числа равна 4. Какой может быть сумма цифр квадрата, этого числа? (Найдите все ответы и докажите, что других ответов нет.)

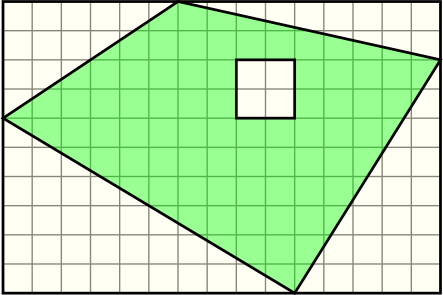
Докажите, что площадь закрашенной фигуры (четырёхугольник с дыркой) равна половине площади большого прямоугольника.

Петя хочет переписать числа 2, 3, 4, ..., 51, в другом порядке так, чтобы первое выписанное число делилось на 1, второе — на 2, третье — на 3, и так далее (последнее число должно делиться на 50). Сколькими способами он может это сделать?

На полке стоят 10 томов собрания сочинений А.П. Чехова, в таком порядке: 1, 2, 3, 4, 5, 6, 7, 8, 10, 9 (два последних тома переставлены местами). Разрешается вытащить любые три стоящих подряд тома и вставить их, не меняя порядка, между любыми двумя книгами или с краю. Можно ли за несколько таких операций расставить все тома по порядку?

Имеется некоторое количество гирь, масса, каждой гири не превосходит 10 кг. Известно, что при любом разбиении всех гирь на две кучки масса хотя бы одной из кучек не превосходит 10 кг. Найдите наибольшую возможную общую массу всех гирь.

Нарисуйте на листе 11 одинаковых квадратов, не налегающих друг на друга, так чтобы при любой раскраске квадратов в 3 цвета какие-то 2 квадрата одного цвета имели общий участок границы.

На бумажной полоске записано 30-значное число без нулей. Полоску разрезают в нескольких местах (между соседними цифрами), и она распадается на, части с числами. Докажите, что всегда найдутся хотя бы два разных способа разрезать полоску так, чтобы сумма получившихся чисел будет одной и той же. (Способы считаются разными, если какой-то разрез в одном способе есть, а в другом — нет.)