Вступительные испытания в школу № 179 (Москва), 7 класс, 2017 год, 3 тур
дата проведения: 3 апреля 2017
Задача 6.
Нарисуйте на листе 11 одинаковых квадратов, не налегающих друг на друга, так чтобы при любой раскраске квадратов в 3 цвета какие-то 2 квадрата одного цвета имели общий участок границы.
Ответ на Задачу 6.
Ответ:
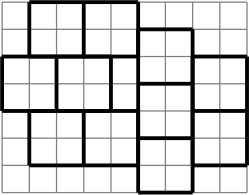
Решение:
Пусть мы используем три цвета: красный, зелёный и синий. Два верхних левых квадрата должны быть покрашены в разные цвета, пусть это красный и зелёный. Тогда однозначно восстанавливается раскраска левой половины рисунка:
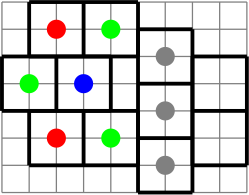
Заметим, что квадраты, отмеченные серым на рисунке выше, не могут быть зелёными. Тогда, чтобы они были раскрашены по правилам, их надо красить их через один красным и синим, например так:
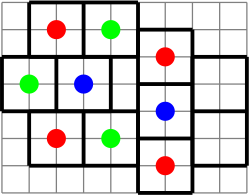
В любом случае крайние правые квадраты тогда оба должны быть зелёные — противоречие. Значит, трёхцветной раскраски не существует.

