Задача 7.
На тетрадном листе отмечены:
- 10 точек на одной прямой;
- три точки в вершинах треугольника.
Разрешается сложить лист бумаги несколько раз по прямой так, чтобы отмеченные точки не попали на линии сгиба, и затем шилом проколоть сложенный лист насквозь. Для каждого из случаев а) и б) докажите, что можно добиться, чтобы дырки оказались в точности в отмеченных точках и лишних дырок не получилось.
Ответ на Задачу 7.
Решение:
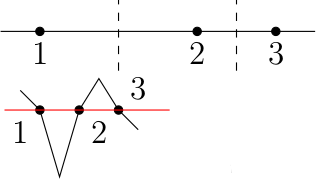
а) Согнем лист «гармошкой», места сгиба — серединные перпендикуляры идущих подряд отрезков (изображены пунктиром; следующий рисунок — «полусогнутый» вид сбоку).
б) Предположим сначала, что какие-то две стороны треугольника ABC не равны. Проведём серединный перпендикуляр к третьей стороне (к AB), он не проходит ни через одну вершину, и пересекает сторону AC в точке H.
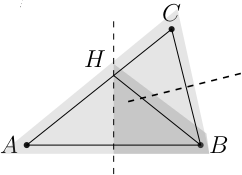
Подвернём края бумаги вокруг сторон треугольника так, чтобы она не высовывалась дальше, чем на 1/100 самого короткого из получившихся на сторонах треугольника отрезков (на нашей картинке это отрезок HC). Теперь можно сложить лист по этому перпендикуляру, и две отмеченные точки A и B наложатся, а над точкой C не будет лишней бумаги. После этого можно сложить лист по серединному перпендикуляру к отрезку BC, в результате точки A, B и C совпадут, а других точек над ними нет.
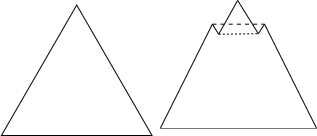
Если же треугольник правильный (все стороны равны), то можно сделать небольшую «складку» (см. рисунок), тогда получившийся треугольник уже не будет равносторонним.