Вступительные испытания в школу № 179 (Москва), 7 класс, 2017 год, 1 тур
дата проведения: 18 марта 2017
Задача 6.
Квадрат 7 × 7 разрезали на части, среди которых не встречается никаких других фигурок, кроме изображённых на рисунке (возможно, повёрнутых или перевёрнутых).
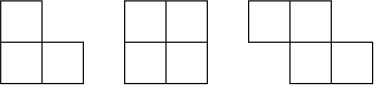
- Приведите пример такого разрезания.
- Докажите, что в любом таком разрезании встречается ровно одна четырёхклеточная фигурка.
Ответ на Задачу 6.
Решение:
a) Например, так:

б) Раскрасим нашу доску 7 × 7 так, как показано на рисунке:

Закрашенных клеток на ней ровно 16. Заметим, что любая из трёх данных фигурок закрывает не более одной закрашенной клетки, и следовательно, нужно не менее 16 фигурок. Но в каждой фигурке минимум 3 клетки, что уже даёт минимум 16 · 3 = 48 клеток из имеющихся 49. Значит, фигурок ровно 16, и оставшаяся клетка принадлежит ровно одной из этих фигурок, которая и будет единственной четырёхклеточной.

