Задача 1.
Расставьте дроби $\frac{4}{5}$, $\frac{15}{19}$, $\frac{19}{24}$ в порядке возрастания и объясните ваш ответ.
Задача 2.
Требуется приготовить 2 яйца всмятку и 4 яйца вкрутую. Яйцо всмятку варится 2 минуты, а вкрутую — 4 минуты (яйца кладут в кипящую воду). За какое наименьшее время это можно сделать, если есть кастрюлька с кипящей водой вместимостью 4 яйца? (Не забудьте объяснить, как сварить яйца за найденное вами время и почему сварить яйца быстрее не получится.)
Задача 3.
Каждому трёхзначному числу, в записи которого участвуют только цифры 1, 2, 3, сопоставили одну из букв А, Б, В по таким правилам:
- числу 111 сопоставили букву А;
- числу 222 сопоставили букву Б;
- числу 133 сопоставили букву А;
- если два числа различаются во всех разрядах, то им сопоставили разные буквы.
Требуется узнать:
- Какую букву по этим правилам сопоставили числу 333?
- А какую — числу 123? Не забудьте обосновать ответы.
Задача 4.
Докажите неравенство ТРИ ⋅ ШЕСТЬ < ТРИДЦАТЬ, где каждая буква обозначает цифру, причём разным буквам соответствуют разные цифры, одинаковым — одинаковые.
Задача 5.
На каждой клетке доски 8 × 8 стоит кубик 1 × 1 × 1. У каждого кубика одна грань чёрная, а остальные — белые. За один ход разрешается проткнуть спицей целиком один ряд (строку или столбец), вынуть его, повернуть вокруг спицы, вставить обратно и вытащить спицу. Всегда ли можно за несколько таких ходов повернуть все кубики чёрными гранями вверх, как бы они не были расставлены изначально?
Задача 6.
Квадрат 7 × 7 разрезали на части, среди которых не встречается никаких других фигурок, кроме изображённых на рисунке (возможно, повёрнутых или перевёрнутых).
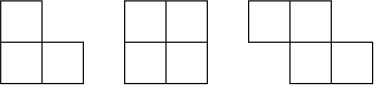
- Приведите пример такого разрезания.
- Докажите, что в любом таком разрезании встречается ровно одна четырёхклеточная фигурка.

