Задача 1.
Кошка Мурка съедает банку "Вискас" за 6 минут, а кот Васька – в 2 раза быстрее. За какое время они съедят банку "Вискас" вместе?
Задача 2.
Яблоко весит столько же, сколько два персика, а три персика – столько же, сколько две груши. Вес трёх слив равен весу одной груши. Что тяжелее – два яблока или семь слив?
Задача 3.
Принесли пять чемоданов и пять ключей от них. Сколько проб достаточно, чтобы подобрать ключ к каждому чемодану?
Задача 4.
Известно, что в Москве каждый двадцатый пятиклассник пришёл на Олимпиаду. А среди московских участников Олимпиады – каждый пятнадцатый – пятиклассник. Кого в Москве больше: пятиклассников или участников олимпиады?
Задача 5.
Пятиклассник Петя перемножил все числа от 1 до 2001. У полученного числа он посчитал сумму цифр, затем посчитал сумму цифр результата, и так далее, пока не получил число, состоящее из одной цифры. Какое?
Задача 6.
Сорок восемь конфет разложены по трём кучкам. Коля переложил из первой кучки во вторую столько конфет, сколько в этой второй кучке первоначально было. Затем из второй переложил в третью столько, сколько в третьей уже было. Наконец, из третьей переложил в первую столько конфет, сколько в этой первой кучке было после первого перекладывания. Теперь конфет во всех кучках одинаково. Сколько конфет было в каждой кучке первоначально?
Задача 7.
На стол положили 35 спичек так, как показано на рисунке. Получилась спираль, "закрученная" по часовой стрелке. Переложите четыре спички так, чтобы получилась такая же спираль, закрученная против часовой стрелки.
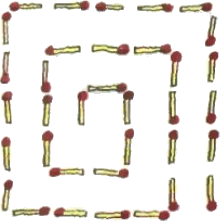
Задача 8.
Разбейте треугольник на четыре треугольника, чтобы каждый из них граничил с каждым (треугольники граничат, если они имеют больше одной общей точки).

