Задача 1.
Лифт поднимается с 1-го этажа на З-й за 7 секунд. За какое время он поднимется с 1-го этажа на 9-й?
Задача 2.
Сколько треугольников ты видишь на рисунке?
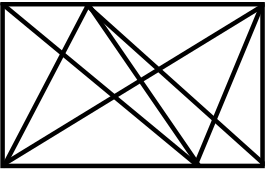
Задача 3.
Петю угощали конфетами. Сначала дали одну конфету. Затем Петя ел имеющиеся у него конфеты по такому принципу: ел конфету, которая у него уже есть, и если она ему нравилась, то ему давали ещё две конфеты, если не нравилась — ел следующую. 25-я конфета Пете не понравилась и конфеты у него кончились. Сколько из 25-и съеденных Петей конфет ему понравились?
Задача 4.
Чебурашка пошёл на день рождения к Крокодилу Гене. Когда он прошёл половину пути, он вспомнил, что забыл дома подарок и вернулся. Поэтому он опоздал к Гене на 20 минут. За какое время Чебурашка мог прийти к Гене, если бы не был таким забывчивым?
Задача 5.
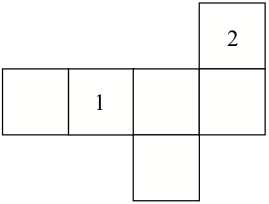
На рисунке изображена развёртка кубика. На ней проставлены только числа 1 и 2. Расставьте остальные числа: 3, 4, 5, 6 так, чтобы сумма чисел на любых двух противоположных гранях была равна 7.
Задача 6.
4М класс играл в снежки. В конце битвы оказалось, что число мальчиков, в которых попали снежком, равно числу девочек, в которых не попали. Кого в классе больше: тех, в кого попали снежком или девочек?
Задача 7.
Кошка Мурка съедает банку "Вискас" за 6 минут, а кот Васька – в 2 раза быстрее. За какое время они съедят банку "Вискас" вместе?
Задача 8.
У 6 школьников одного кружка спросили, сколько лампочек на потолке в кабинете, где проходит кружок. Получили такие ответы:
- первый: больше одной,
- второй: больше двух,
- третий: больше трёх,
- четвёртый: больше четырёх,
- пятый: меньше четырёх,
- шестой: меньше трёх.
Сколько лампочек в кабинете, если ровно половина школьников сказала правду? Найдите все варианты!

