Задача 1.
Голодные Малыш и Карлсон съели торт и стали сытыми. Известно, что голодный Карлсон легче сытого Малыша, а сытый Карлсон весит столько же, сколько два голодных Малыша. Что весит больше: торт или голодный Малыш?
Задача 2.
На устный тур олимпиады пришло 100 школьников. Каждому из них было предложено решить 6 задач. Результаты заносились в таблицу, где за верно решённую задачу ставился «+», а за неверно решённую «–». По результатам тура наградили тех, кто решил 4 и более задачи. Дима посмотрел в таблицу и насчитал 350 «плюсиков». Докажите, что наградили не менее 17 участников.
Задача 3.
У Карабаса-Барабаса украли пять золотых. Карабас подозревает в краже лису Алису, кота Базилио, Дуремара и Буратино, так как неопровержимыми уликами установлено, что:
- кто-то из них обязательно виновен;
- никто больше не мог это сделать;
- Алиса всегда действует заодно с Базилио;
- если Дуремар виновен, то у него было ровно два соучастника;
- если Буратино виновен, то у него был ровно один соучастник.
Нужно определить, виновен ли Базилио.
Задача 4.
В разные моменты времени из пунктов А и В выехали навстречу друг другу велосипедист и мотоциклист. Встретившись в точке С, они тотчас развернулись и поехали обратно. Доехав до своих пунктов, они опять развернулись и поехали навстречу друг другу. На этот раз они встретились в точке D и, развернувшись, вновь поехали к своим пунктам. И т.д. В какой точке отрезка АВ произойдёт их 2006 встреча?
Задача 5.
На рисунке нарисован прямоугольник, который четырьмя отрезками разбит ещё на несколько прямоугольников. Внутри некоторых прямоугольников написаны их периметры. Найдите периметр большого прямоугольника.
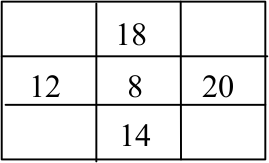
Задача 6.
У Вини-Пуха было 100 горшочков мёда. Кристофер Робин принёс или забрал 9 горшочков, что именно – Пух не помнит. На следующий день Кристофер Робин снова пришёл и принёс или забрал 8 горшочков, на следующий день – 7 и так далее. Наконец Кристофер Робин пришёл и принёс или забрал один горшочек. Сколько горшочков мёда могло быть у Вини-Пуха на 10 день, если все это время он мёд не ел?
Задача 7.
В классе 30 учеников. Они сидят за 15-ю партами. При этом оказалось, что ровно половина всех девочек сидит с мальчиками. Докажите, что их не удастся пересадить (за те же 15 парт) так, чтобы ровно половина всех мальчиков класса сидела с девочками.
Задача 8.
На планете "Куб" (имеющей форму куба) каждой гранью владеет рыцарь (который всегда говорит правду) или лжец (который всегда лжёт). Каждый из них утверждает, что среди его соседей лжецов больше, чем рыцарей. Сколько рыцарей и сколько лжецов владеют гранями планеты?
Задача 9.
Стёпа Иванов решил проверить закон всемирного тяготения. Для этого он сел под яблоней и стал считать яблоки, падающие с дерева. Первый раз он просидел под деревом 12 минут и насчитал 5 яблок, второй раз – 20 минут и насчитал 6 яблок. Теперь он собирается сидеть под яблоней полчаса. Сколько яблок сможет он теперь сосчитать? (известно, что яблоки падают строго через одинаковые промежутки времени)

