Задача 5.
Замок имеет форму правильного треугольника, разбитого на 25 одинаковых залов, каждый из которых также имеет форму правильного треугольника (см. рисунок):
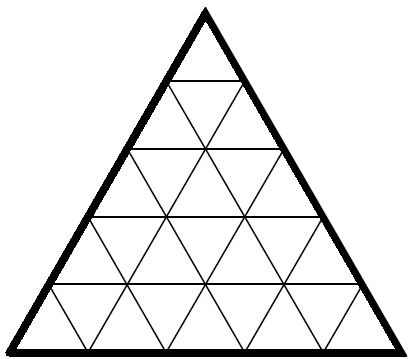
В стене между любыми двумя залами есть дверь. Путник хочет обойти как можно больше залов, не заходя ни в один зал дважды. Какое наибольшее количество залов ему удастся обойти?
Ответ на Задачу 5.
Ответ: 21.
Решение:
Раскрасим план замка так, как на рисунке:
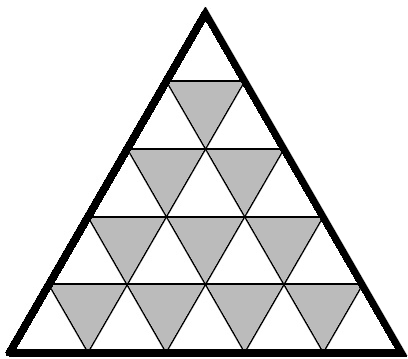
Тогда из условия следует, что путник переходит из белого зала в серый и из серого зала в белый. Если он каждый зал может посетить только один раз, то количество белых и серых залов, посещённых путником, может отличаться не более, чем на 1. Заметим, что белых залов 15, а серых — 10. Тогда число посещённых залов не может быть больше 21 (11 белых + 10 серых). Пример для 21 привести можно (см. рисунок):
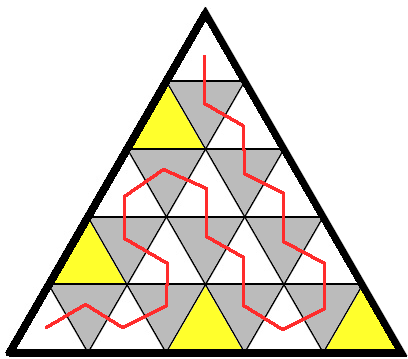
Жёлтым цветом отмечены непосещённые залы.

