Задача 1.
Маша написала на доске четыре натуральных последовательных числа. Лёша разделил каждое из них на 10 и стёр цифры после запятой. Оказалось, что теперь сумма написанных на доске чисел равна 2007. Какие числа написала Маша изначально?
Задача 2.
Про числа $a$, $b$ и $c$ известно, что:
$$\frac{a}{b+c}=\frac{b}{c+a}=\frac{c}{a+b}$$
Докажите, что:
$$\frac{(a+b)^2}{c^2}+\frac{(c+a)^2}{b^2}+\frac{(b+c)^2}{a^2}=6+\frac{a+b}{c}+\frac{c+a}{b}+\frac{b+c}{a}$$
Задача 3.
На рисунке треугольники АВС, СDК и АКМ – равносторонние. Докажите, что АD = МС.
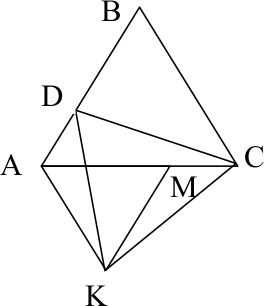
Задача 4.
В комнате сидело 2007 жителей острова рыцарей и лжецов. В какой-то момент один человек обиделся и ушёл. Один из оставшихся, поглядев в след, заметил: «Ушедший – лжец!» После чего встал и тоже вышел. Второй сказал: «Оба ушедшие – лжецы» и тоже ушёл. Далее каждый из оставшихся уходил, говоря: «Все ушедшие – лжецы». Пока последний оставшийся в комнате печально констатировал: «Да, все ушедшие – лжецы». Определите, сколько в комнате было лжецов первоначально. (Лжецы всегда лгут, рыцари всегда говорят правду).
Задача 5.
Замок имеет форму правильного треугольника, разбитого на 25 одинаковых залов, каждый из которых также имеет форму правильного треугольника (см. рисунок):
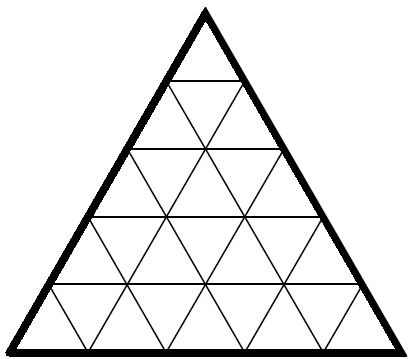
В стене между любыми двумя залами есть дверь. Путник хочет обойти как можно больше залов, не заходя ни в один зал дважды. Какое наибольшее количество залов ему удастся обойти?
Задача 6.
На сторонах AB и BC ромба ABCD с углом A, равным 60°, взяты соответственно точки E и F так, что сумма BE и BF равна стороне ромба. Докажите, что серединный перпендикуляр к отрезку DE проходит через точку F.
Задача 7.
Малыш и Карлсон разрезали круглый торт прямолинейными разрезами, проходящими через его центр, на 22 одинаковых кусков. Они договорились поочерёдно съедать по 2 произвольных куска до тех пор пока не останется два куска, а оставшиеся 2 куска достанутся Малышу, если они окажутся рядом, и Карлсону в противном случае. Начинает есть, конечно, Карлсон. Кто из них сумеет съесть больше торта?
Задача 8.
Половина шахматного поля 6×6 отделена «забором» – главной диагональю. Шахматный конь «пасётся» на одной половине шахматной доски и не может ни наступать на, ни перескакивать через «забор». За час он «съедает всю траву на одной клетке» и должен прыгнуть на другую клетку. Какое максимальное время конь может «пастись на поле», не возвращаясь дважды на одну и ту же клетку?
Задача 9.
В какое наименьшее число цветов необходимо раскрасить числа от 1 до 2007 так, чтобы если одно число делится на другое, то они окрашены в разные цвета?

