Задача 5.
Незнайка купил в магазине 4 одинаковых игральных кубика. Развлекаясь, он решил прикладывать их друг к другу гранями с одинаковым числом очков. В результате на столе появилась следующая конструкция (см. рисунок):
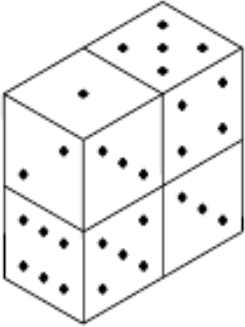
Знайка взглянул на конструкцию Незнайки и заявил, что тот опять что-то напутал. Прав ли Знайка?
Ответ на Задачу 5.
Ответ: прав.
Решение:
Обозначим кубики (1), (2), (3) и (4) как показано на рисунке.
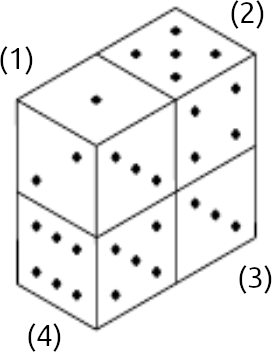
Так как у первого кубика нам видны грани с очками 1, 2 и 3, то кубик (4) не может соприкасаться с кубиком (1) по грани с очками 1, 2 или 3. Но поскольку у кубика (4) видны грани с очками 5 и 6, то если незнайка ничего не напутал, кубики (1) и (4) соприкасаются по грани с четырьмя очками.
Тогда кубик (1) может соприкасаться с кубиком (2) только гранью с 6 очками (поскольку грань с 5 очками у кубика (2) видна). Таким образом, поскольку кубики одинаковые, то они устроены так: противоположные грани 1 и 4, 2 и 6, 3 и 5. Но тогда кубик (2) должен соприкасаться с кубиком (3) гранью с 3 очками (как противоположной верхней грани с 5 очками), что невозможно.

