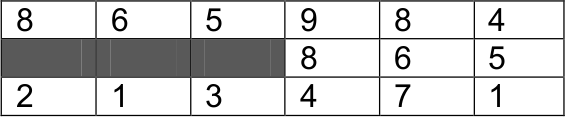
Олимпиада начальной школы 2x2, 3 класс, 2010 год
дата проведения: 7 марта 2010
Задача 5.
Замените в выражении буквы цифрами от 1 до 9 так, чтобы получились верные неравенства (одинаковые буквы = одинаковые цифры, разные буквы = разные цифры).
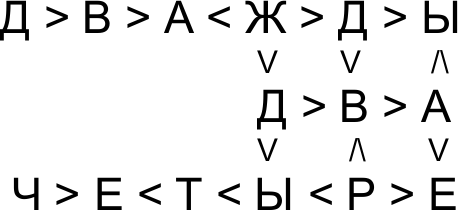
Ответ на Задачу 5.
Решение:
Понятно, что задача решается небольшим перебором. Наша цель – минимизировать этот перебор. Посмотрим, где может стоять цифра «1» (наименьшее число). Это не А (оно больше, чем Е), это не Ы (оно больше, чем Т). Похоже, что это Е. Проверим: Е меньше, чем А, В, Д, Р, Ы, Т, Ч и чем Ж, так как Ж больше А. Это 8 цифр. Значит, наш выбор верен и Е = 1. Аналогично, можно убедиться, что Ж = 9 (наибольшее число). Далее возможно несколько вариантов. Один из них приведён на рисунке.