Олимпиада начальной школы 2x2, 5 класс, 2010 год, 2 тур
дата проведения: 7 февраля 2010
Задача 5.
Числа от 1 до 9 расставлены по кругу, как показано на рисунке.
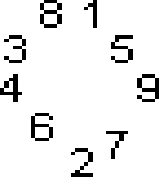
Можно сколько угодно раз менять местами любые два из них, которые дают одинаковый остаток при делении на 3. Можно ли в итоге получить расстановку этих чисел по порядку?
Ответ на Задачу 5.
Ответ: Нельзя.
Решение:
Заметим, что когда мы меняем местами 2 числа, порядок остатков при делении на 3 не меняется. У правильно упорядоченной последовательности порядок остатков при делении на 3 таков: 1;2;0;1;2;0;1;2;0. Для данной последовательности: 1;2;0;1;2;0;1;0;2. В ней с обеих сторон от одной из цифр 1 стоят нули. Значит, правильного порядка после разрешённых замен не получится.

