Ответ: 5 человек.

Решение:

Очевидно, что если есть дедушка и внуки, то есть и отец, и сыновья. Уже имеем 3 сыновей (папа – сын дедушки, и два внука – сыновья папы) и двух отцов (дедушка – отец папы, и сам папа). Для выполнения условия не хватает одного сына и одного отца. Это не может быть ни ещё один внук, ни ещё один дедушка, так как тогда бы не выполнялось условие. Значит это ещё один сын дедушки и ещё один отец одного из детей. Поскольку у одного ребёнка не может быть двух отцов, то каждый внук имеет своего отца.

Окончательный вариант: дедушка, его два сына, у каждого из которых есть сын. Всего 5 человек.

Комментарий: существует также другой вариант (ниже), который тоже считается верным.

Ответ 2: дедушка, его брат, у них есть сыновья, у каждого по одному. У сына дедушки ещё есть два сына, то есть два внука дедушки (итого 6 человек).

Решение 2: Изобразим на рисунке:

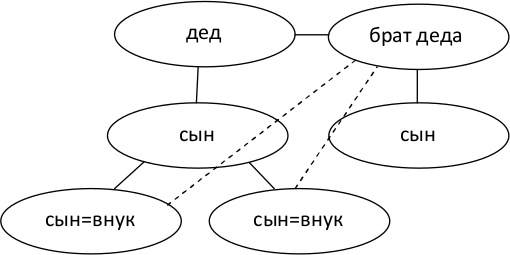
В этом варианте решения справедливо полагается, что брат деда не является дедушкой для внуков брата. То есть двоюродный дедушка дедушкой не считается.