Олимпиада начальной школы 2x2, 6 класс, 2011 год, 2 тур
дата проведения: 22 мая 2011
Задача 7.
𝑁-конём назовём фигуру, которая ходит буквой Γ со сторонами 1 и 𝑁. Найдите все такие 𝑁, что на бесконечной доске несколькими ходами 𝑁-коня можно дойти из любой клетки в любую другую.
Ответ на Задачу 7.
Ответ: Все чётные числа.
Решение:
Сначала покажем, что нечётные 𝑁 не годятся. Действительно, покрасив доску в шахматную раскраску, заметим, что при ходе 𝑁-конь не меняет цвет поля. Значит, попасть на клетку другого цвета не удастся.
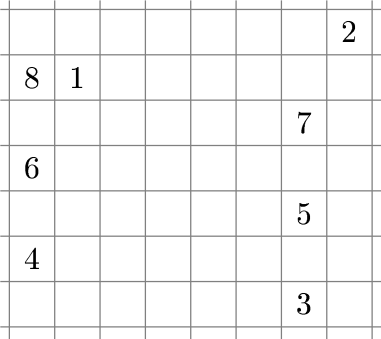
Теперь покажем, что для любого чётного 𝑁 можно попасть на любое другое поле. Для этого достаточно научиться попадать на соседнюю клетку. Покажем, как попасть на соседнюю по горизонтали клетку. На картинке показано, как это сделать для 𝑁 = 6. Аналогично можно сделать для любого чётного 𝑁.