Маша составила два числа: в одном были только единицы и семерки, а в другом — только двойки и тройки, причём в каждом из чисел не все цифры были одинаковы. Могло ли так быть, что одно из этих чисел делится на другое?

Гриша взял бумажный треугольник и вырезал из него квадрат (см. рисунок).

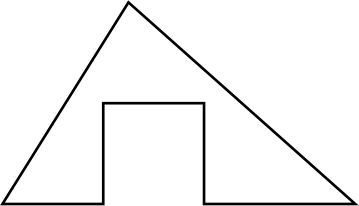
Известно, что периметр треугольника был равен 17, а периметр полученной фигуры 23. Найдите площадь новой фигуры, если площадь треугольника была равна 25.

На поляне собрались несколько больших и несколько маленьких барсуков (причём были и те, и другие). Каждый большой барсук сказал, что маленьких барсуков больше двух, а каждый маленький — что больших больше двух. Сколько барсуков могли сказать неправду?

Когда троллейбус выехал из автобусно-троллейбусного парка, то троллейбусов в парке осталось 1/4 от всего транспорта в нём. Но когда троллейбус вернулся в парк, троллейбусы стали составлять уже треть всего транспорта. Сколько автобусов было в парке, если известно, что пока троллейбус следовал по маршруту, ни один автобус и ни один троллейбус не выехал и не въехал в парк?

Существует ли компания из 10 человек такая, что у каждого человека было бы ровно три знакомых и у любых двух незнакомых был бы ровно один общий знакомый?

В футбольном турнире, проходящем в два этапа, участвуют 16 команд. В первом этапе все команды играют между собой двухкруговой турнир (каждая команда с каждой играет два матча). Во втором этапе первые восемь команд играют между собой двухкруговой турнир, и последние восемь команд играют между собой двукруговой турнир. Какая наибольшая разница очков может быть между очками первой команды первой восьмёрки и первой команды второй восьмёрки в конце турнира, если за победу в каждом матче даётся 3, за ничью — 1 и за поражение — 0 очков (очки после первого этапа сохраняются)?

𝑁-конём назовём фигуру, которая ходит буквой Γ со сторонами 1 и 𝑁. Найдите все такие 𝑁, что на бесконечной доске несколькими ходами 𝑁-коня можно дойти из любой клетки в любую другую.

В школе работает несколько секций, всего больше 15 секций, в каждой не более 15 мест. Известно, что для любых 16 секций найдётся ученик, который записался во все эти секции. Докажите, что тогда есть ученик, который записался во все секции.

Иван нарисовал пятиугольник и в его вершинах написал 5 различных натуральных чисел. Затем на каждой стороне этого пятиугольника он написал наименьшее общее кратное чисел, написанных в вершинах этой стороны и заметил, что все записанные на сторонах пять чисел равны. Какое наименьшее число могло оказаться на сторонах?