Задача 6.
Маша умножила число само на себя и получила четырёхзначное число. Так случилось, что цифры сотен и тысяч в полученном числе равны. Также равны цифры единиц и десятков. Какое число умножала Маша?
Ответ на Задачу 6.
Ответ: 88.
Решение:
Полученное произведение будет иметь вид ААВВ. Это значит, что оно делится на 11. Но тогда и исходное число должно было делиться на 11. Поэтому нужно проверить числа 11, 22, 33, 44, 55, 66, 77, 88, 99. Число 110 и больше проверять уже не нужно, поскольку результат будет пятизначным и больше. Аналогично не нужно рассматривать числа 11 и 22, так как для них произведения трехзначны. Далее можно проверить оставшиеся числа путём возведения в квадрат.
Комментарий: Для школьников, знакомых с делимостью, можно предложить более короткое решение. ААВВ=11×А0В, причём второй множитель также делится на 11. Это значит, что, продолжая деление столбиком, получим (см. рисунок), где В+С=10.
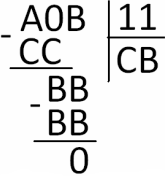
Но СВ – это квадрат однозначного числа (3, 4, 5, 6, 7, 8 или 9). Выпишем квадраты: 9, 16, 25, 36, 49, 64, 81. Только два последних удовлетворяют условию. Проверкой убеждаемся, что это 64.

