Олимпиада начальной школы 2x2, 5 класс, 2013 год, 1 тур
дата проведения: 27 января 2013
Задача 3.
Виталик написал на грани кубика 1, повернул и на соседней грани написал 2, затем вновь повернул и написал 3, и т.д. Так он пронумеровал все грани кубика числами от 1 до 6. Какая максимальная сумма может быть у номеров двух противоположных граней?
Ответ на Задачу 3.
Ответ: 10.
Решение:
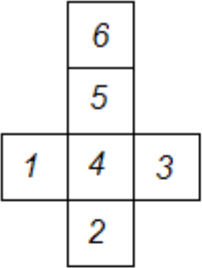
Максимальная сумма двух различных натуральных чисел от 1 до 6 равна 5+6=11, причём любая другая пара чисел, очевидно, даёт меньшую сумму. Однако числа 5 и 6 по условию задачи стоят на соседних гранях кубика, значит, суммы 11 добиться нельзя. Можно ли добиться суммы 10? Оказывается да. На рисунке числа 4 и 6 находятся на противоположных гранях и их сумма равна 10. А путь от 1 до 6 проходит по соседним граням.