Задача 4.
Прямоугольный участок периметра 4 км разбит на 4 прямоугольных участка садоводов, а в центре построен бассейн. Каков периметр бассейна, если суммарная длина парадных ворот (отмечено на рисунке жирным) равна 1700 м?
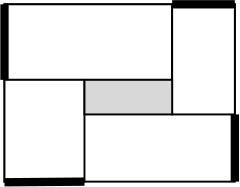
Ответ на Задачу 4.
Ответ: 600м.
Решение:
Представим, что мы построили новые парадные ворота – парадные ворота в пруд (также отмечены жирным на новом рисунке). Заметим, что длина парадных ворот в пруд равна половине периметра пруда.
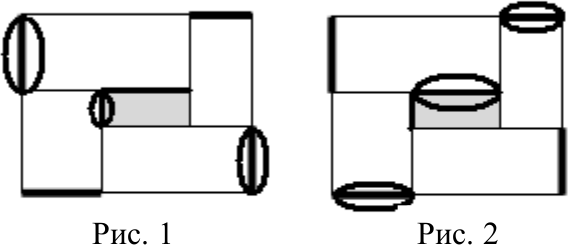
Теперь чтобы решить задачу посчитаем половину периметра участка двумя способами.
Первый способ. Периметр участка равен 4 км, значит, половина периметра равна 2 км (2000 м).
Второй способ. Общая длина парадных ворот (как старых, так и новых) равна половине периметра. Действительно отрезки, выделенные на рис. 1 в сумме дают одну сторону участка, а отрезки, выделенные на рис. 2 в сумме дают другую сторону участка.
Итак, 2000 м = общая длина парадных ворот = длина старых ворот + длина новых = 1700 м + длина новых = 1700 м + половина периметра пруда. Таким образом, 2000 м = 1700 м + половина периметра пруда, а значит половина периметра пруда = 300 м. Соответственно периметр пруда равен 600 м.

