Задача 2.
На клетчатой бумаге нарисовали пятиугольник и частично закрасили его серым цветом (см. рисунок).
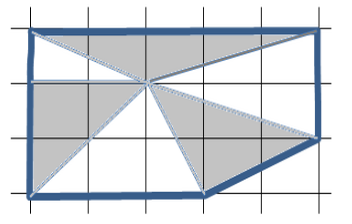
Какая часть пятиугольника имеет большую площадь: закрашенная или незакрашенная?
Ответ на Задачу 2.
Ответ: Площади равны.
Решение 1: Разделим исходную фигурку на 4 части, как на рисунке.
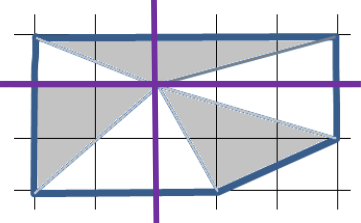
Тогда легко видеть, что в трёх частях линия делит прямоугольник пополам – на белый и серых треугольники. Рассмотрим оставшуюся часть:
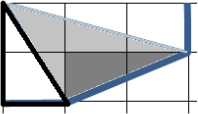
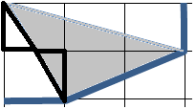
Заметим, что тёмный и выделенный белый треугольники равны. Кроме того равны маленькие треугольники на втором рисунке и, значит, равны площади серого белого выделенного кусков:
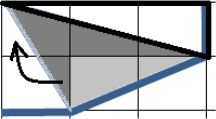
Решение 2: Площадь всего пятиугольника равна площади прямоугольника размером 3×5 клеток без половины прямоугольника 1×2 клетки. То есть площадь пятиугольника равна 14. Площади белых треугольников вычисляются и в сумме дают 7. Значит, на серую часть также приходится 7 клеток.

