Можно ли числа 3, 1, 0, 1, 2, 0, 1, 6 расставить в вершинах куба так, чтобы суммы чисел на всех рёбрах были различны?

На клетчатой бумаге нарисовали пятиугольник и частично закрасили его серым цветом (см. рисунок).

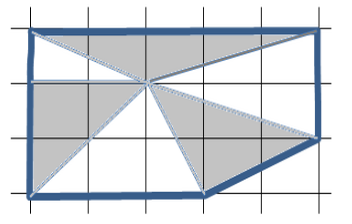
Какая часть пятиугольника имеет большую площадь: закрашенная или незакрашенная?

Кощей Бессмертный решил собрать сундук изумрудов и в первый день положил в пустой сундук 1 изумруд. На следующий день положил туда 2 изумруда и так далее – каждый следующий день он клал в сундук на 1 изумруд больше, чем в предыдущий. Однако во вторую ночь Баба Яга стащила из сундука 1 изумруд и каждую следующую ночь тащила на 1 изумруд больше. Как только в сундуке наберётся 2016 изумрудов, Кощей его запечатает и спрячет, и баба Яга не сможет красть. На какой день это произойдёт?

На день рождения Карлсон получил коробку шоколадных конфет. Кристер съел меньше всех конфет, а Гунилла – больше всех. Малыш съел чётное число конфет, в 3 раза больше, чем Кристер и в 2 раза меньше Гуниллы. Все остальные конфеты съел Карлсон. Могло ли в коробке быть 65 конфет?

Паша, Коля, Лёша и Саша сыграли в шахматном турнире в один круг (каждый с каждым по одной партии). Оказалось, что все набрали разное количество очков, и ничьих не было. После турнира каждый высказался:

• Паша: Я набрал больше всех очков.
• Коля: У Лёши очков больше, чем у Паши.
• Лёша: У Коли и Паши столько же очков в сумме, сколько и у Саши.
• Саша: Мой результат лучше результата Лёши.

Определите, кто какое занял место в турнире, если известно, что все солгали. (За победу в шахматах даётся 1 очко, за проигрыш – 0)