Задача 4.
На день рождения Карлсон получил коробку шоколадных конфет. Кристер съел меньше всех конфет, а Гунилла – больше всех. Малыш съел чётное число конфет, в 3 раза больше, чем Кристер и в 2 раза меньше Гуниллы. Все остальные конфеты съел Карлсон. Могло ли в коробке быть 65 конфет?
Ответ на Задачу 4.
Ответ: Не могло.
Решение:
Пусть Кристер съел какую-то часть конфет, тогда Малыш съел в 3 раза больше, чем Кристер. То есть три таких части. Так как по условию Малыш съел чётное число конфет, то будем считать, что он съел 6х, тогда Кристер 2х, а Гунилла – 12х. Тогда все вместе они съели 20х конфет. А Карлсон съел все остальное, то есть 65 – 20х. При этом Карлсон должен был съесть меньше Гуниллы и больше Кристера. То есть меньше 20х и больше 2х. 2х < 65 – 20x < 12x.
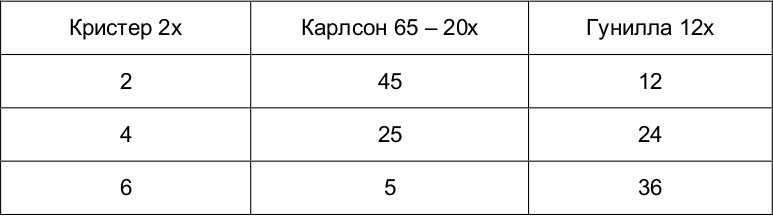
Остальные случаи невозможны. Но и эти случаи не подходят, поскольку в первых двух Карлсон съел больше Гуниллы, а в последнем – меньше Кристера.

