Задача 6.
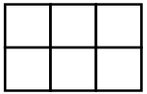
Из квадратных карточек выложили прямоугольник (на рисунке ниже пример прямоугольника из 6 карточек). Потом одну его сторону уменьшили в 2 раза, а другую в 3. При этом освободилось 65 карточек. Сколько квадратов со стороной 4 карточки можно было выделить из исходного прямоугольника, не перекладывая карточки? (на рисунке можно выделить 2 квадрата со стороной 2 карточки)
Ответ на Задачу 6.
Ответ: Ни одного.
Решение:
Заметим, что в результате описанных действий площадь прямоугольника уменьшилась в 6 раз. Возможные случаи нарисованы на рисунках (закрашенный прямоугольник – тот, что получился).
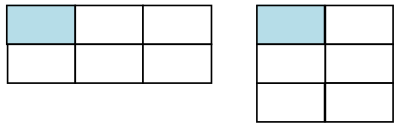
Таким образом площадь оставшегося прямоугольника = 65 : 5 = 13 карточек. Но из 13 карточек можно составить только один прямоугольник размером 1х13 карточек. Значит, изначальный прямоугольник был размером 2х39 карточек или 3х26 карточек. В обоих случаях одна из сторон меньше 4 карточек и ни один квадрат со стороной 4 карточки выделить нельзя.

