Задача 6.
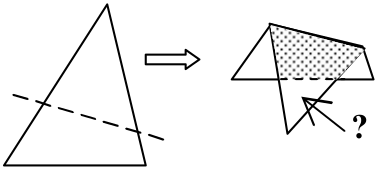
В бумажном треугольнике провели отрезок, делящий площадь треугольника пополам, а затем сложили по этой линии. Оказалось, что площадь «двуслойной части» (серая на рисунке) равна площади «однослойной части» и на 12 см2 меньше площади исходного треугольника. Найдите площадь нижнего маленького треугольника.
Ответ на Задачу 6.
Ответ: 3 см2.
Решение 1: Обозначим части 𝑎, 𝑏, 𝑐 и 𝑑.
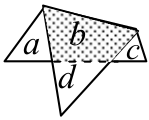
Из первого условия следует, что 𝑎 + 𝑏 + 𝑐 = 𝑏 + 𝑑, или 𝑎 + 𝑐 = 𝑑. Из второго следует, что 𝑏 = 𝑎 + 𝑐 + 𝑑, то есть 𝑏 = 2𝑑. Также из второго условия получаем 𝑎 + 𝑐 + 𝑑 = 𝑎 + 2𝑏 + 𝑐 + 𝑑 – 12 (обе части равны 𝑏), откуда 𝑏 = 6. Тогда 𝑑 = 3.
Решение 2: Сгибая треугольник, мы уменьшаем его площадь на площадь двухслойной части. Значит, площадь серой фигуры равна 12. Поскольку треугольник разбили на две одинаковые по площади части, то площадь каждой части равна площади одной и той же серой фигуры + один или два треугольника. То есть площадь нижнего треугольника равна сумме площадей двух других. А в сумме их площади равны площади серой фигуры.

