Задача 4.
Костя сложил фигуру из трёх шестиугольников и записал во всех вершинах числа, как на рисунке (в центральной вершине тоже записал число – неизвестно какое).
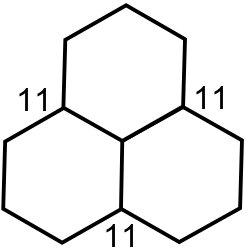
Потом Костя увеличил числа в вершинах одного шестиугольника на одно и то же число, потом увеличил числа в вершинах второго шестиугольника на одно и то же число (возможно, другое), а затем проделал то же самое с третьим шестиугольником. Вот некоторые числа, которые у него получились.
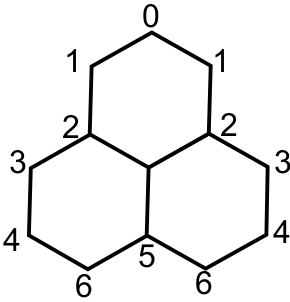
На сколько изменилось число в центральной вершине?
Ответ на Задачу 4.
Ответ: На 12.
Решение:
Заметим, что когда мы увеличиваем числа в вершинах какого-то шестиугольника, то мы увеличиваем на одно и то же число числа в двух вершинах из отмеченных (рисунок слева) и центральной. Можно считать, что мы увеличиваем не сразу на данное число, а несколько раз на 1. Тогда сумма в трёх отмеченных вершинах увеличивается в два раза быстрее, чем число в центре. Всего сумма чисел в трёх вершинах увеличилась на (11−2)+(11−2)+(11−5) = 24. Это значит, что число в центральной вершине увеличилось на 24:2 = 12.

