Задача 5.
На острове Ромба живут рыцари и лжецы (рыцари говорят только правду, лжецы всегда лгут). В каждой треугольной области живёт ровно 1 человек, соседними считаются области, граничащие по стороне.
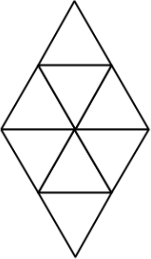
Утром каждый из них сказал: «Среди моих соседей не более 1 рыцаря». Какое наибольшее число рыцарей может проживать на острове?
Ответ на Задачу 5.
Ответ: 6 рыцарей
Решение:
Сказанное в условии означает, что среди соседей либо 0, либо 1 рыцарь. Поэтому в самой верхней и самой нижней области не могут жить лжецы, ведь у них всего 1 сосед и в любом случае не может быть более 1 рыцаря. Поэтому там живут рыцари. Далее заметим, что в выделенных цветом фигурках из 3 треугольников не могут жить по 3 рыцаря, ведь тогда у среднего будут хотя бы два соседа рыцаря.
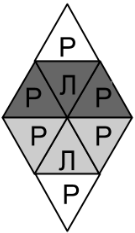
Значит, там живут не более 2 рыцарей, а всего рыцарей 2 + 2∙2 = 6. Пример на рисунке выше.

