Буквы А, И, Б, О сидели на трубе. Одна буква упала с трубы один раз, другая − два раза, а остальные попадали по три раза. Сколько раз упала с трубы буква А, если буква И упала не три раза, буквы А и Б падали разное количество раз и буквы О и Б падали разное количество раз?

У Гарри в пробирке ёмкостью 2 мл налито 1 мл вещества А, в пробирке ёмкостью 4 мл налито 4 мл вещества В, в пробирке ёмкостью 7 мл налито 7 мл вещества С. Известно, что если в равных пропорциях смешать два разных вещества, то получится третье. Если же пропорции будут неравные, то будет взрыв. Гарри нужно получить по 4 мл каждого вещества. Как ему это сделать, если у него ещё есть пустая пробирка ёмкостью 2 мл? Все пробирки волшебные − вещество можно полностью вылить и следов не останется. Делений на пробирках нет.

В квадрате со стороной 4 нарисовали ещё один квадрат с вершинами в серединах сторон. Две середины сторон разных квадратов соединены отрезком (см. рисунок):

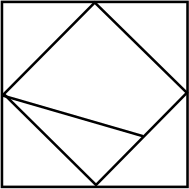
Найдите площадь квадрата, сторона которого равна этому отрезку.

Коля положил на стол несколько кубиков белого, синего, красного, зелёного и чёрного цвета в ряд. Оказалось, что для любых двух цветов найдётся пара кубиков этих цветов, которые лежат рядом. То есть есть белый и красный кубики, лежащие рядом, зелёный и белый кубики, лежащие рядом, а так для любой пары цветов. Какое минимальное количество кубиков может лежать на столе?

На острове Ромба живут рыцари и лжецы (рыцари говорят только правду, лжецы всегда лгут). В каждой треугольной области живёт ровно 1 человек, соседними считаются области, граничащие по стороне.

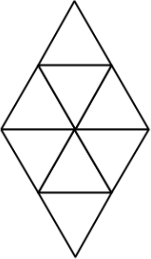
Утром каждый из них сказал: «Среди моих соседей не более 1 рыцаря». Какое наибольшее число рыцарей может проживать на острове?