Задача 6.
Разрежьте клетчатую доску по линиям сетки на несколько (меньше, чем 15) одинаковых кусочков, в каждом из которых все числа были бы разные.
Ответ на Задачу 6.
Ответ: на рисунке.
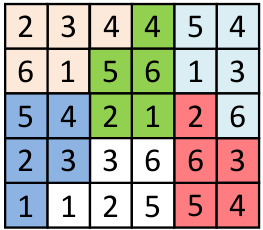
Решение:
Поскольку кусочков должно быть меньше 15, то разрезать нужно на фигурки из 3, 5 или 6 клеток. Больше клеток в фигурке быть не может, так как тут всего 6 разных цифр. Докажем, что разрезать на уголки из 3 клеток не получится. Предположим, что можно. Тогда в левом нижнем углу уголок только 1-2-3.
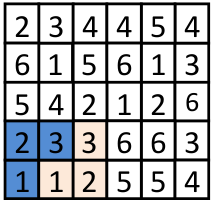
Так как иначе либо изолирована угловая клетка, либо две единицы в одном уголке. Но тогда в следующем квадратике две шестёрки, две пятёрки и уголок с разными цифрами вырезать не получится. Можно ли разрезать исходный прямоугольник на требуемые фигурки из 6 клеток или полоски из 3 клеток − оставляем читателю для самостоятельного исследования.

