Задача 8.
Можно ли клетчатую фигуру на рисунке разрезать по линиям сетки на три одинаковые части? Если можно, то как, если нельзя, то почему.
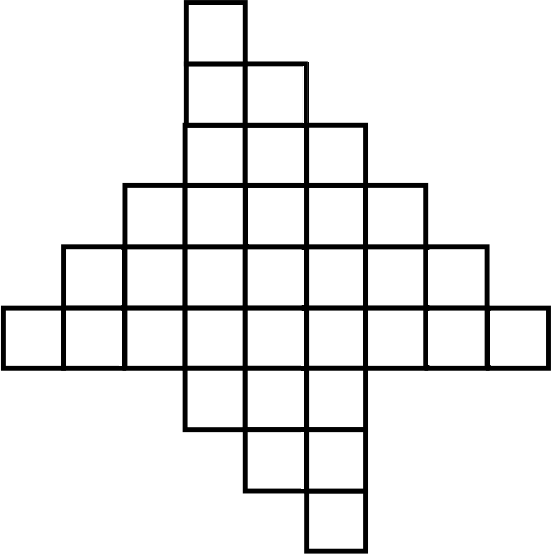
Ответ на Задачу 8.
Ответ: Нельзя.
Решение:
Раскрасим нашу фигуру в шахматном порядке.
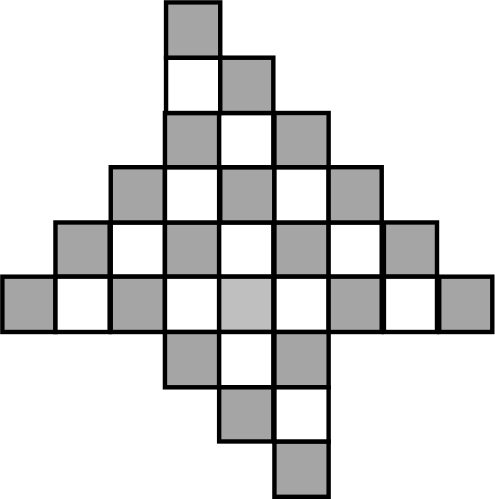
Тогда чёрных клеток 20, белых 13 Это означает, что три полученные фигуры одинаково покрашены быть не могут − тогда количество и чёрных, и белых клеток делилось бы на 3. Поэтому две фигуры покрашены одним способом, а одна фигура покрашена другим, «реверсированным» способом, в котором чёрные клетки находятся на месте белых, а белые − на месте чёрных. Пусть в фигуре А чёрных и В белых клеток, тогда получается, что А + В = 33/3 = 11. Но ещё 2А + В = 20 чëрных клеток, а А + 2В = 13 белых клеток Получаем А = 9, В = 2. Получается, в фигуре всего две белых клетки и целых девять чёрных Но так как фигура связная, то рядом с каждой чёрной клеткой должна быть белая, но у двух белых клеток всего 8 сторон. Противоречие.

