Задача 1.
В стране ДваЖдыДва города называются буквами русского. Жители страны заметили, что их девиз «БезМатематикиЖитьНельзя» точно описывает связь между городами: если какие-то буквы стоят рядом, то значит эти города соединены дорогой. К примеру город Ь соединён дорогой с городами Т, Н, Л и З. Можно ли объехать все города страны ДваЖдыДва, побывав в каждом ровно один раз? (Все города страны перечислены в девизе)
Задача 2.
В ряд стоит 4 человека, среди которых 3 рыцаря и 1 лжец. Любому человеку можно задать вопрос: «среди твоих соседей есть лжец?» Как, задав 2 таких вопроса и услышав ответы, точно определить, кто из четверых является лжецом?
Задача 3.
На доске написано 9 букв: П О М П О Н Ч И К. Катя заменяет каждую букву на какую-то цифру, причём разные буквы она заменила на разные цифры, а одинаковые буквы – на одинаковые цифры. После этого Оксана хочет поставить между некоторыми буквами (возможно, не всеми) знак «+» так, чтобы получился пример на сложение с чётным результатом. Докажите, что Оксана всегда сможет этого добиться.
Задача 4.
Из клетчатого квадрата 5×5 вырезали одну клетку, как на рисунке.

От этого периметр фигуры увеличился. Какое минимальное количество клеток нужно ещё вырезать, чтобы периметр полученной фигуры стал таким, как прежде?
Задача 5.
Филипп написал на оконном стекле фломастером четырёхзначное число. Оказалось, что если посмотреть на окно с другой стороны, то там тоже будет четырёхзначное число. Филипп решил вычесть из большего меньшее и получил 2373. Какие числа были написаны на стекле?

Задача 6.
Имеются волшебные фрукты: яблоки, груши и бананы. Антон, Вася и Саша взяли себе по одному фрукту. Известно, что тот, у кого банан, лжёт тому, у кого яблоко. Тот, у кого яблоко, лжёт тому, у кого груша. Тот, у кого груша, лжёт тому, у кого банан. В остальных случаях все говорят правду. Антон сказал человеку с яблоком: «У Васи банан». Вася ответил Антону: «Неправда! У меня груша». Какие фрукты взяли ребята?
Задача 7.
Можно ли расположить на плоскости два неравных квадрата так, чтобы все расстояния между вершинами одного квадрата и вершинами другого были равны либо стороне меньшего квадрата, либо стороне большего квадрата?
Задача 8.
Можно ли клетчатую фигуру на рисунке разрезать по линиям сетки на три одинаковые части? Если можно, то как, если нельзя, то почему.
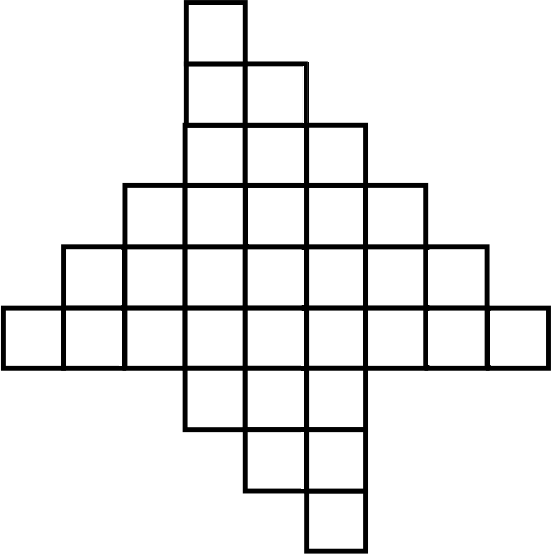
Задача 9.
На дне квадратной коробки 11×11 в один слой уложены 60 «доминошек» размером 1×2. При этом получилась одна свободная клетка. Люда закрашивает свободную клетку дна коробки маркером, если можно сдвинуть какую-то «доминошку», сдвигает и закрашивает ещё одну клетку дна коробки и так далее. Останавливается Люда только тогда, когда покрасила все клетки дна коробки, до которых вообще возможно добраться. Какое максимальное количество клеток она могла закрасить?

