Задача 10.
Однажды 11 жителей Острова рыцарей и лжецов встали в необычный хоровод, как на рисунке. Каждый заявил: «Среди моих соседей поровну рыцарей и лжецов!». Сколько могло быть рыцарей среди собравшихся? Укажите все возможные варианты. (Рыцарь всегда говорит правду, лжец всегда лжёт)
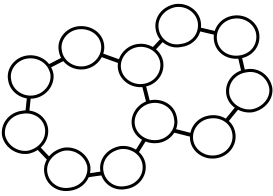
Ответ на Задачу 10.
Ответ: 0 или 4.
Решение:
У двух жителей на пересечении кругов по 3 соседа, значит, каждый из них не может иметь поровну соседей-рыцарей и соседей-лжецов. Значит, оба они лжецы.
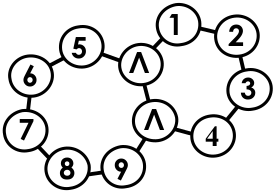
Рыцарей может не быть вообще, этот вариант подходит. Если рыцари есть, то можно заметить, что они обязаны стоять парами. Если рыцарь имеет в соседях двух лжецов,то он сказал ложь. Если есть три подряд идущих рыцаря, то средний рыцарь лжёт. Значит 1 2 3 4 все лжецы. Т.к. если на 1 2 пара рыцарей, то на 3 лжец скажет правду. Если на 2 3 пара рыцарей, то лжец на 4 скажет правду. Если на 3 4 пара рыцарей, то лжец на 2 скажет правду. С другим кругом. Если 7 рыцарь, то парный ему рыцарь находится на 6 или на 8. Если на 6, то тогда лжец на 5 скажет правду. Если на 8, то лжец на 9 скажет правду. Значит, 7 не может быть рыцарем. Рассмотрим пары 6-5 и 8-9 Если это две пары рыцарей, то этот вариант подходит. Если же в одной паре, например, в 6-5 есть лжец, то и второй из этой пары лжец Аналогично для пары 8-9.

