Задача 1.
В дате 29 января Коля заменил все буквы числами − номером буквы в русском алфавите − и получил число 293315311833. Вычеркните в этом числе 5 цифр так, чтобы получилось:
- наибольшее из возможных семизначных чисел;
- наименьшее из возможных семизначных чисел.
Задача 2.
Сегодня 29 января. Петя вырезал из картона цифры 2 и 9 и наклеил их на лист, как на рисунке. Двумя прямыми разрезами разделите картонные цифры на 9 кусочков.

Задача 3.
Федя разложил 20 орехов на три тарелки (не все на одну) так, что седьмая часть орехов на первой тарелке равна пятой части орехов на второй тарелке. Сколько орехов лежит на третьей тарелке?
Задача 4.
Саша посылает в телеграм сообщения Маше каждые 2 минуты. Маша проверяет телефон каждые 5 минут. Папа написал и запустил на телефон Саши вирус, который запускается каждые 3 минуты и удаляет все сообщения Саши, которые есть в данный момент. Если вирус включается в тот же момент, что Саша пишет сообщение, то вирус не даёт его отправить. Ровно в полдень Саша начал писать сообщения, а Маша − проверять телефон. И в тот же момент первый раз включился вирус. Сколько сообщений получит Маша к 14:00?
Задача 5.
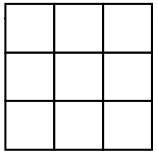
Расставьте в клетках таблицы 3×3 числа от 1 до 9 так, чтобы сумма чисел в каждом квадратике 2×2 давала при делении на 4 разные остатки.
Задача 6.
У Буратино был блокнот, сшитый из 25 двойных листов в их середине. Все страницы пронумерованы числами от 1 до 100. Буратино вырвал 17 двойных листов и заново пронумеровал страницы получившегося блокнота, написав числа рядом с предыдущими. В результате на одной странице оказалось написано число 523. Какое число может быть написано на бывшей 94 странице, если известно, что она не вырвана?
Задача 7.
Разрежьте фигуру на рисунке на 3 равные части.

Задача 8.
У Кирилла есть 12 карточек: 3 жёлтых, 2 голубых, 2 синих, 1 оранжевая, белая карточка с цифрой 0, две карточки со знаком умножения и одна карточка со знаком равенства. Напишите на пустых карточках цифры (на каждой карточке одну цифру) и составьте из всех карточек верное равенство так, чтобы на карточках одного цвета были написаны одинаковые цифры, а на карточках разных цветов − разные.

Задача 9.
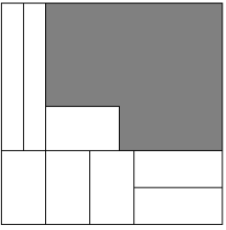
Гоша нарисовал квадрат, а потом разбил его на несколько прямоугольников одинаковой площади. Затем он закрасил целиком несколько прямоугольников так, что их границы стали не видны, а остальные прямоугольники на рисунке остались (см. рисунок). Сколько прямоугольников закрасил Гоша?
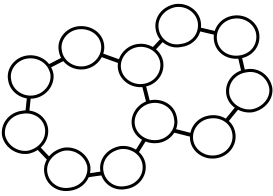
Задача 10.
Однажды 11 жителей Острова рыцарей и лжецов встали в необычный хоровод, как на рисунке. Каждый заявил: «Среди моих соседей поровну рыцарей и лжецов!». Сколько могло быть рыцарей среди собравшихся? Укажите все возможные варианты. (Рыцарь всегда говорит правду, лжец всегда лжёт)