Задача 5.
Во всех клетках квадратной таблицы 5 × 5 написаны числа. Известно, что сумма всех чисел равна 77. В любой фигурке из трёх клеток вида 
сумма чисел равна 10 (фигурку можно поворачивать). Найдите сумму чисел, написанных:
в угловых клетках таблицы;
в клетках, выделенных серым цветом на рисунке.
Комментарий: числа могут быть отрицательными.
Ответ на Задачу 5.
Ответ: а) 7; б) 11.
Решение:
а) Если отрезать от квадрата угловые клетки, то оставшуюся фигуру можно разрезать на 7 прямоугольников 1 × 3 и 3 × 1 (см. рисунок).
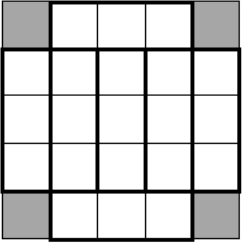
Поэтому сумма чисел в угловых клетках квадрата равна 77 − 7 ⋅ 10 = 7.
б) Прибавив к сумме чисел в серых клетках сумму чисел в 6 прямоугольниках на первом рисунке ниже (4 фиолетовых и 2 перекрывающихся), получим сумму чисел во всех клетках плюс удвоенное число центральной клетки. Вычитая из суммы всех чисел сумму чисел в 8 прямоугольниках на втором рисунке ниже, найдём число в центральной клетке: 77 − 8 ⋅ 10 = −3.
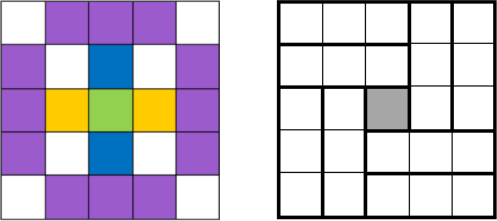
Тогда сумма чисел в серых клетках равна 77 − 6 ⋅ 10 + 2 ⋅ (−3) = 11.
