Бельчонок празднует свой день рождения 4-го февраля. Чтобы хорошо отдохнуть, он лёг спать в полдень 17 января. В полдень в среду он проснулся, сразу же заснул снова, проспал в два раза дольше и проснулся в полдень 4-го февраля. На какой день недели приходится день рождения бельчонка?

На доске записано число 679854, в котором использованы 6 последовательных цифр. Найдите следующее за ним большее число, в записи которого также используются 6 последовательных цифр (может быть, других).

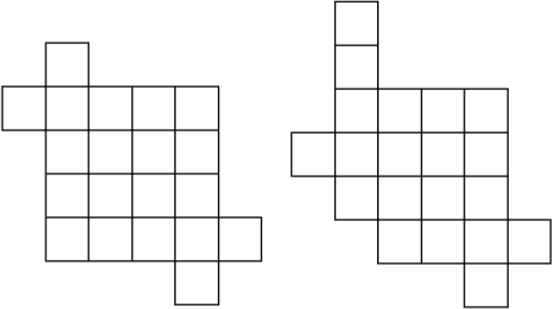
Разрежьте фигуру, изображённую на рисунке слева, на две равные части и покажите, как сложить из этих частей фигуру, изображённую на рисунке справа. Части считаются равными, если их можно точно совместить при наложении друг на друга, при этом их можно переворачивать и поворачивать.

Утром ученики 6А, 6Б классов в рамках зимней универсиады пошли смотреть биатлон, а ученики 6В, 6Г — лыжные гонки. Оказалось, что на биатлоне было на 15 шестиклассников больше, чем на лыжных гонках. Вечером 6А и 6В пошли в кино, а 6Б и 6Г – в театр. Оказалось, что в кино было на 8 шестиклассников меньше, чем в театре. Могло ли такое быть?

Во всех клетках квадратной таблицы 5 × 5 написаны числа. Известно, что сумма всех чисел равна 77. В любой фигурке из трёх клеток вида сумма чисел равна 10 (фигурку можно поворачивать). Найдите сумму чисел, написанных:

1. в угловых клетках таблицы;

2. в клетках, выделенных серым цветом на рисунке.

Комментарий: числа могут быть отрицательными.