Олимпиада «Бельчонок», 5 класс, 2019-2020 год, 1 этап, 1 вариант
дата проведения: 1 октября 2019 - 13 января 2020
Задача 2.
На рисунке изображены три окружности и одна прямая, которые пересекаются в сумме в 6 отмеченных точках. В каком наибольшем количестве точек в сумме могут пересекаться три окружности и одна прямая?
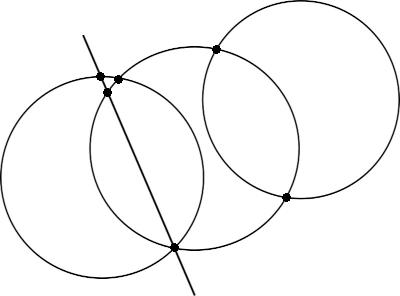
Ответ на Задачу 2.
Ответ: 12 точек.
Решение:
Две окружности могут пересекаться максимум в 2 точках. Третья окружность может пересечь первую окружность в 2 точках и вторую окружность в 2 точках, итого три окружности могут пересекаться максимум в 6 точках. Прямая может пересечь каждую окружность в 2 точках, то есть ещё плюс 6 точек. Итого 12 точек.

