Задача 5.
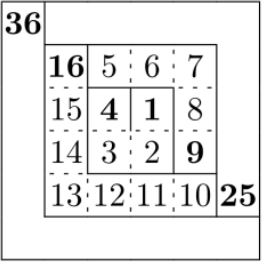
Вася расставляет в клетки бесконечного клетчатого листа по спирали натуральные числа, начиная с 1 (см. рисунок). Какое число будет написано в клетке справа от числа 521?
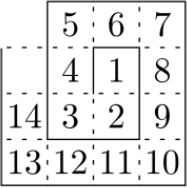
Ответ на Задачу 5.
Ответ: 616.
Решение:
В тот момент, когда Вася выписывает число $n^2$, заполненные клетки образуют квадрат $n$ × $n$. Из алгоритма выписывания чисел ясно, что числа вида $n^2$ при четном $n$ расположены в диагонали, идущей влево и вверх от клетки с числом 4, а при нечётном $n$ – в диагонали, идущей вправо и вниз от клетки с числом 1. Поскольку 222 = 484 < 521 < 529 = 232, число 529 было выписано в процессе формирования квадрата со стороной 23. Так как 529 − 521 = 8, число 521 находится на правой стороне этого квадрата на 8 клеток выше его правой нижней угловой вершины 529. Соседнее справа число находится на 9 клеток выше угловой клетки квадрата со стороной 25, содержащей число 252 = 625. Значит, соседнее число равно 616.